Kompetenzorientierung im Fach Mathematik

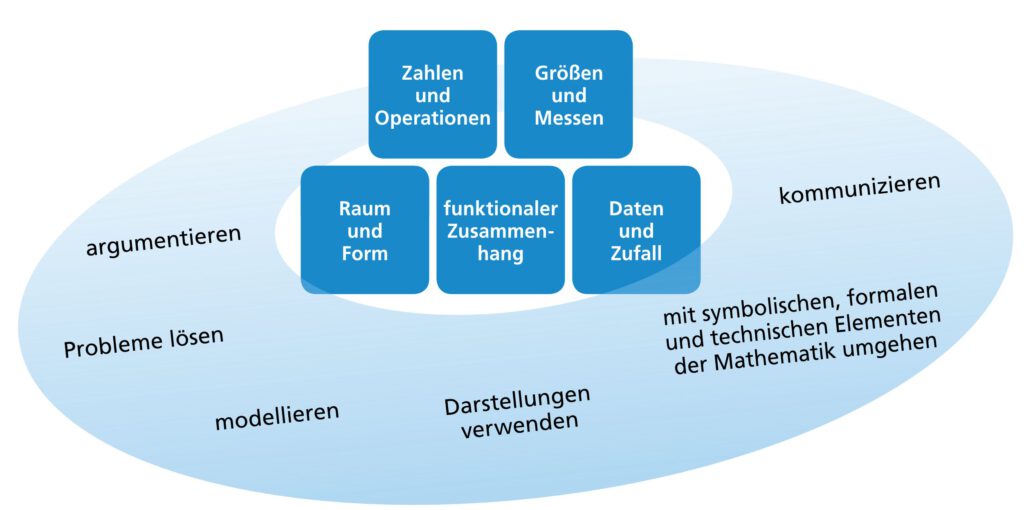
Kompetenzstrukturmodell Mathematik

 

Das dem Lehrplan zugrunde liegende Kompetenzstrukturmodell orientiert sich an den Bildungsstandards im Fach Mathematik für die Primarstufe, für den Mittleren Schulabschluss und für die Allgemeine Hochschulreife (2003, 2004 und 2012) der Kultusministerkonferenz. Es unterscheidet zentrale Aspekte mathematischen Arbeitens, die als prozessbezogene allgemeine mathematische Kompetenzen beschrieben werden (äußerer Ring), und konkrete mathematische Inhalte, die nach Gegenstandsbereichen geordnet sind (innere Felder).

Die allgemeinen mathematischen Kompetenzen werden von den Schülerinnen und Schülern in aktiver Auseinandersetzung mit den mathematischen Inhalten – also nicht isoliert davon – erworben und angewandt. Entsprechend lassen sich die allgemeinen mathematischen Kompetenzen vielfältig inhaltsbezogen konkretisieren, wobei in der Regel an jedem Fachinhalt alle allgemeinen mathematischen Kompetenzen entwickelt werden können.

 

Förderung von Kompetenzen im Unterricht

Von entscheidender Bedeutung für die Entwicklung mathematischer Kenntnisse, Vorstellungen, Fähigkeiten und Fertigkeiten ist es, die Schülerinnen und Schüler zu vertieftem Nachdenken und intensiver Auseinandersetzung mit den Lerninhalten anzuregen. Diese kognitive Aktivierung ist Voraussetzung für den Erwerb mathematischer Kompetenzen. Wesentlich hierfür sind die eingesetzten Fragen und Aufgaben sowie deren Einbettung in den Unterricht. Gute Aufgaben bieten ein breites Spektrum im Hinblick auf die Art der Fragestellung, den Kontext und das Anforderungsniveau, sie wecken Interesse und regen die Schülerinnen und Schüler zur Reflexion sowie zur selbständigen Beschäftigung mit Mathematik an.

Kognitive Aktivierung ist weitgehend methodenunabhängig und lässt sich in verschiedenen Arbeits- und Sozialformen erreichen. Die Variation der Unterrichtsmethoden bietet jedoch einen günstigen Rahmen für die Entwicklung mathematischer Kompetenzen und hat positive Effekte auf die Motivation der Lernenden.

Kennzeichen eines guten Mathematikunterrichts ist eine Unterrichtsatmosphäre, die es begünstigt, dass sich die Schülerinnen und Schüler von mathematischen Fragestellungen angesprochen fühlen. Die Berücksichtigung von Vorerfahrungen sowie ein altersgemäßes Anknüpfen an die Lebenswelt der Kinder und Jugendlichen sind dafür unerlässlich. Erfolgreicher Mathematikunterricht setzt Prinzipien wie kumulatives, vernetzendes und entdeckendes Lernen, systematisches Wiederholen sowie Lernen aus Fehlern um. Die verschiedenen Unterrichtsinhalte müssen von den Schülerinnen und Schülern über die Jahre hinweg bewusst aufeinander bezogen und miteinander verknüpft werden können. Dadurch wird ihnen ihr persönlicher Lernzuwachs deutlich, wodurch auch ihre Motivation wächst.

Guter Mathematikunterricht muss dabei auch die Entwicklung grundlegender manueller mathematischer Fertigkeiten sowie die Festigung grundlegender Kenntnisse im Blick haben und stellt deshalb regelmäßig geeignete Aufgaben bereit, die von den Schülerinnen und Schülern ohne elektronische Hilfsmittel (z. B. Taschenrechner, Software) bzw. ohne Merkhilfe oder Formelsammlung zu bearbeiten sind.

 

Quelle: https://www.lehrplanplus.bayern.de/fachprofil/gymnasium/mathematik